개념 정리/중1
2.2 정수와 유리수의 계산 - 두 수의 덧셈, 덧셈의 연산법칙, 두 수의 뺄셈, 덧셈과 뺄셈의 혼합 계산, 덧셈과 뺄셈의 활용
NumbeRings
2024. 5. 6. 15:11

두 수의 덧셈
부호가 같은 두 수의 덧셈
두 수의 절댓값의 합에 공통인 부호를 붙인다.
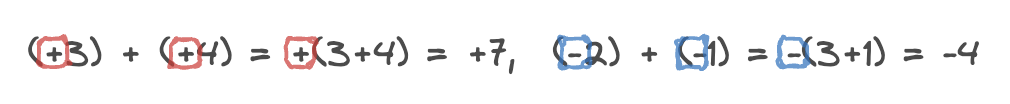
(공통인 부호)(절댓값의 합)
부호가 다른 두 수의 덧셈
두 수의 절댓값의 차에 절댓값이 큰 수의 부호를 붙인다.

(절댓값이 큰 수의 부호)(절댓값의 차)
어떤 수와 0의 덧셈
어떤 수와 0의 합은 그 수 자신이다.
(+3) + 0 = +3
유리수의 덧셈
- 분모가 다른 두 분수의 덧셈은 분모의 최소공배수로 통분하여 계산한다.
- 분수와 소수의 덧셈은 소수를 분수로 바꾸어 통분하거 나 분수를 소수로 바꾸어 계산한다.
- 절댓값이 같고 부호가 다른 두 수의 합은 0이다.
덧셈의 연산 법칙
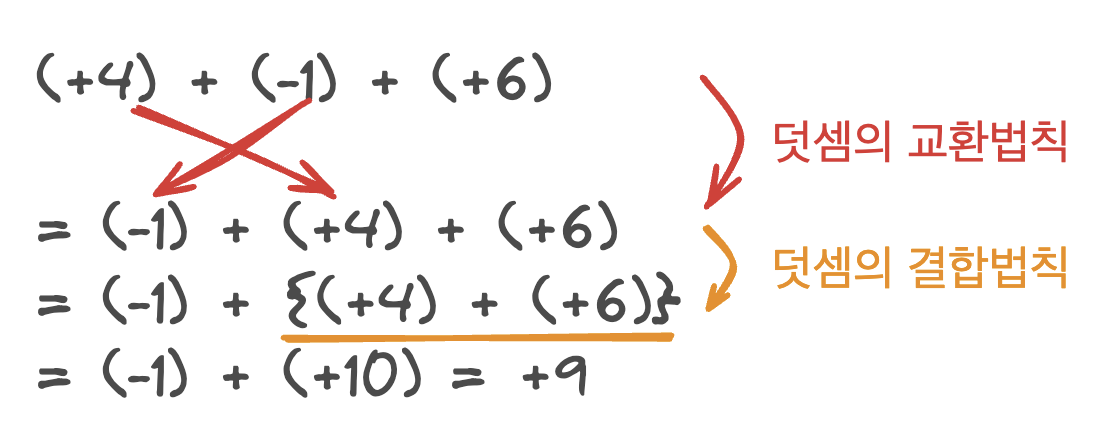
세 수 a, b, c에 대하여
- 덧셈의 교환법칙: a + b = b + a
- 덧셈의 결합법칙:(a + b) + c = a + (b + c)
세 수의 덧셈에서는 덧셈의 결합법칙이 성립하므로 (a + b) + c, a + (b + c)를 모두 a + b + c로 나타낼 수 있다.
두 수의 뺄셈
두 수의 뺄셈은 빼는 수의 부호를 바꾸어 덧셈으로 고쳐서 계산한다.

뺄셈에서는 교환법칙과 결합법칙이 성립하지 않는다.
5 - 2 $\neq$ 2 - 5
5 - 3 - 1 $\neq$ 5 - (3 - 1)
덧셈과 뺄셈의 혼합 계산
덧셈과 뺄셈의 혼합 계산
- 뺄셈을 모두 덧셈으로 고친다.
- 덧셈의 교환법칙과 결합법칙을 이용하여 양수는 양수끼리, 음수는 음수끼리 모아서 계산한다.
분수가 있는 식은 분모가 같은 것끼리 모아서 계산하면 편리하다.
부호가 생략된 수의 혼합 계산
부호가 생략된 수의 혼합 계산은 + 부호와 괄호를 살려서 계산한다.
-8 + 3 = (-8) + (+3) = -5
생략된 부호 + 넣기
덧셈과 뺄셈의 활용
●보다 ■만큼 큰(작은) 수
1. ●보다 ■만큼 큰 수 → ● + ■
a보다 1만큼 큰 수 → a + 1
a보다 -1만큼 큰 수 → a + (-1)
2. ●보다 ■만큼 작은 수 → ● - ■
a보다 1만큼 작은 수 → a - 1
a보다 -1만큼 작은 수 → a - (-1)
덧셈과 뺄셈 사이의 관계
1. ● + ■ = ▲ → ● = ▲ - ■
■ = ▲ - ●
2. ● - ■ = ▲ → ● = ▲ + ■
■ = ● - ▲