
수직선
직선 위에 기준이 되는 점 O를 잡고, 그 점에 수 0을 대응시킨다. 점 O의 좌우에 일정한 간격으로 점을 잡고, 점 O의 오른쪽 점에 양의 정수를, 왼쪽 점에 음의 정수를 차례로 대응시킨 직선을 수직선이라 한다.
→ 모든 유리수는 수직선 위의 점에 대응시킬 수 있다.
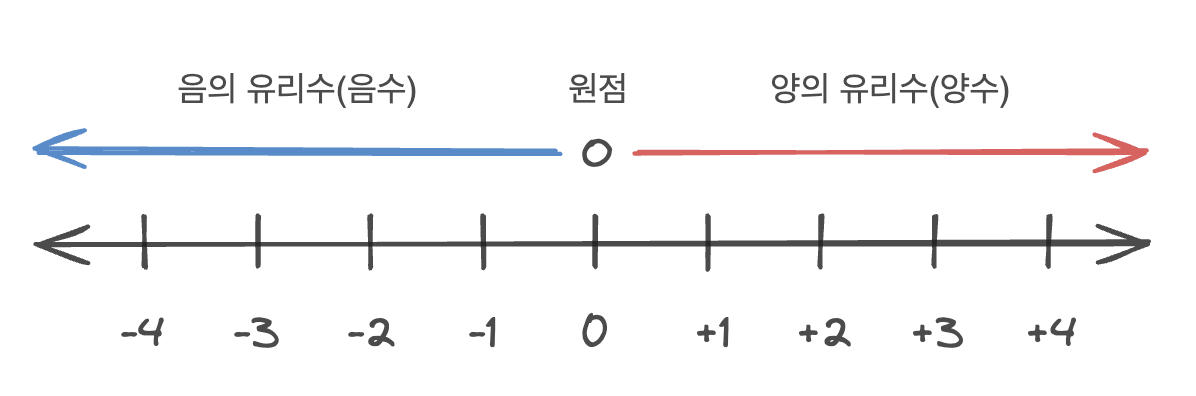
수직선에서 수 0에 대응하는 기준이 되는 점 O를 원점이라 한다.
절댓값
절댓값
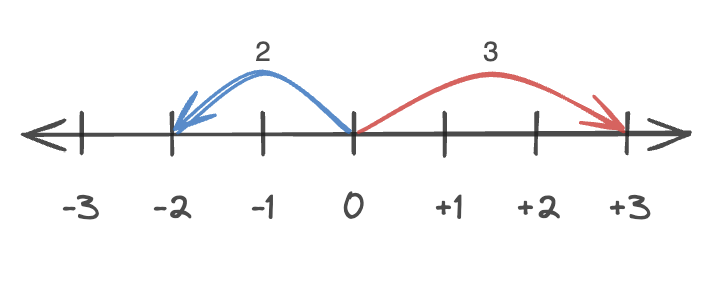
수직선 위에서 원점과 어떤 수에 대응하는 점 사이의 거리
유리수 a의 절댓값 → |a|
+3의 절댓값: |+3| = 3
-2의 절댓값: |-2| = 2
절댓값의 성질
- 양수와 음수의 절댓값은 그 수의 부호 +, -를 떼어 낸 수와 같다.
- 0의 절댓값은 0이다. 즉, |0| = 0
- 절댓값은 항상 0 또는 양수이다.
- 원점에서 멀리 떨어질수록 절댓값이 커진다.
수의 대소 관계

수직선 위에서 수는 오른쪽으로 갈수록 커지고, 왼쪽으로 갈수록 작아진다.
1. 양수는 0보다 크고, 음수는 0보다 작다. 즉, (음수) < 0 < (양수)
-3 < 0, -3 < +2, 0 < +2
2. 두 양수끼리는 절댓값이 큰 수가 크다.
+12 > +9
3. 두 음수끼리는 절댓값이 큰 수가 작다.
-5 < -2
'개념 정리 > 중1' 카테고리의 다른 글
| 2.2 정수와 유리수의 계산 - 두 수의 덧셈, 덧셈의 연산법칙, 두 수의 뺄셈, 덧셈과 뺄셈의 혼합 계산, 덧셈과 뺄셈의 활용 (0) | 2024.05.06 |
|---|---|
| 2.1 정수와 유리수 - 부등호의 사용 (0) | 2024.05.06 |
| 2.1 정수와 유리수 - 양수와 음수, 정수와 유리수, 유리수의 분류 (0) | 2024.05.06 |
| 1.2 최대공약수와 최소공배수 - 최대공약수와 최소공배수의 관계 (0) | 2024.05.05 |
| 1.2 최대공약수와 최소공배수 - 최소공배수의 활용 (0) | 2024.05.05 |



