2.2 정수와 유리수의 계산 - 두 수의 곱셈, 곱셈의 연산법칙, 세 수 이상의 곱셈, 거듭제곱의 계산, 분배법칙, 두 수의 나눗셈, 역수를 이용한 나눗셈

2.2 정수와 유리수의 계산 - 수의 곱셈과 나눗셈

두 수의 곱셈

부호가 같은 두 수의 곱셈

두 수의 절댓값의 곱에 양의 부호 +를 붙인다.

두 수의 곱셈

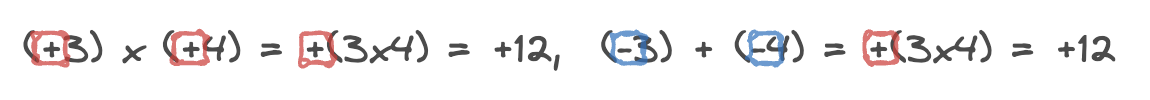
(양의 부호)(절댓값의 곱)

 

부호가 다른 두 수의 곱셈

두 수의 절댓값의 곱에 음의 부호 -를 붙인다.

두 수의 곱셈

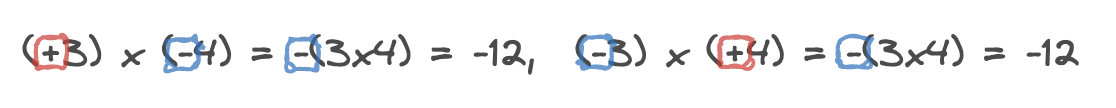
(음의 부호)(절댓값의 곱)

 

어떤 수와 0의 곱셈

어떤 수와 0의 곱은 항상 0이다.

(+3) x 0 = 0

 

곱셈의 부호

• ( + ) x ( + ) = ( + )
• ( - ) x ( - ) = ( + )
• ( + ) x ( - ) = ( - )
• ( - ) x ( + ) = ( - )

 

곱셈의 연산 법칙

곱셈의 연산 법칙

세 수 a, b, c에 대하여

1. 곱셈의 교환법칙: a x b = b x a
2. 곱셈의 결합법칙: (a x b) x c = a x (b x c)

세 수의 곱셈에서는 곱셈의 결합법칙이 성립하므로 (a x b) x c, a x (b x c)를 모두 a x b x c로 나타낼 수 있다.

 

세 수 이상의 곱셈

1. 먼저 곱의 부호를 정한다. 이때 곱해진 음수의 개수가

• 짝수 개이면 → +
• 홀수 개이면 → -

    2. 각 수의 절댓값의 곱에 1. 에서 결정된 부호를 붙여서 계산한다.

 

세 수 이상의 곱셈

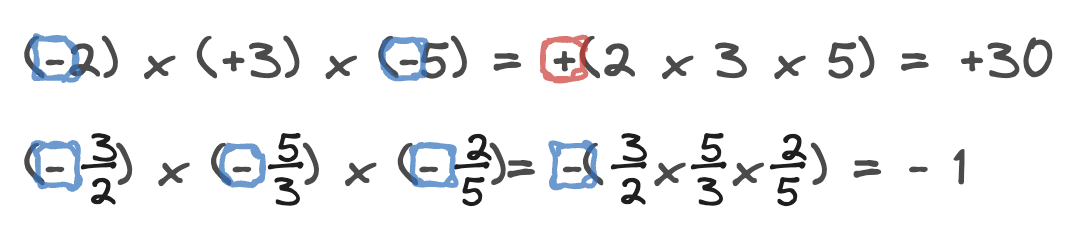
음수가 짝수 개면, 부호는 +
음수가 홀수 개면, 부호는 -

 

세 수 이상의 곱셈

( - ) x ( - ) x ( - ) = ( + ) x ( - ) = ( - )

거듭제곱의 계산

양수의 거듭제곱의 부호

→ 항상 양수

(+2)² = (+2) x (+2)= +(2 x 2) = +4
(+2)² = (+2) x (+2) x (+2) = +(2 x 2 x 2) = +8

 

음수의거듭제곱의부호

→ 지수가

• 짝수 개이면 → +
• 홀수 개이면 → -

(-2)² = (-2) x (-2)= +(2 x 2) = +4
(-2)² = (-2) x (-2) x (-2) = -(2 x 2 x 2) = -8

(-2)²과 -2²을 혼동하지 않도록 한다.
(-2)² = (-2) x (-2) = 4
-2² = -(2x2) = -4

 

분배법칙

어떤 수에 두 수의 합을 곱한 것은 어떤 수에 각각의 수를 곱하여 더한 것과 그 결과가 같다. 이것을 분배법칙이라 한다.

즉, 세 수 a, b, c에 대하여

a x (b + c) = a x b + a x c, (a + b) x c = a x c + b x c

분배법칙

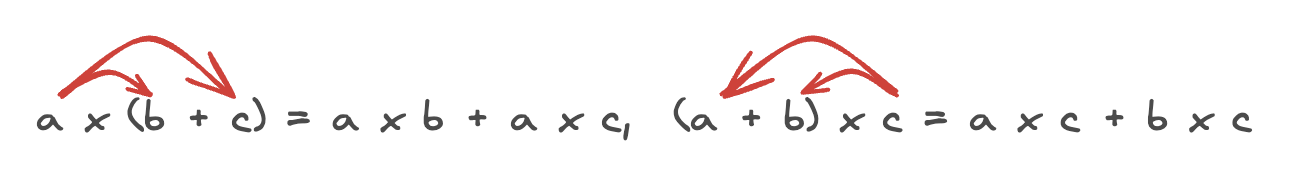
분배법칙을 이용하여 괄호 풀기 → 3 x 105 = 3 x (100 + 5) = 3 x 100 + 3 x 5
분배법칙을 이용하여 괄호 묶기 → 2 x 55 + 2 x 45 = 2 x (55 + 45) = 2 x 100

 

두 수의 나눗셈

부호가 같은 두 수의 나눗셈
두 수의 절댓값의 나눗셈의 몫에 양의 부호 +를 붙인다.

두 수의 나눗셈

(양의 부호)(절댓값의 나눗셈의 몫)

 

부호가 다른 두 수의 나눗셈

두 수의 절댓값의 나눗셈의 몫에 음의 부호 -를 붙인다.

두 수의 나눗셈

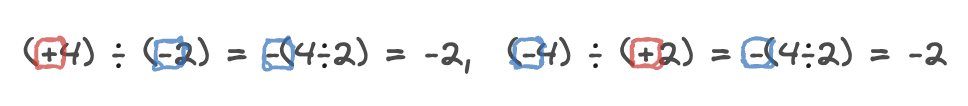
(음의 부호)(절댓값의 나눗셈의 몫)

 

0의 나눗셈

0을 0이 아닌 수로 나누면 그 몫은 항상 0이다. 예

0 $\div$ (+3) = 0

 

나눗셈의 부호

• ( + ) $\div$ ( + ) = ( + )
• ( - ) $\div$ ( - ) = ( + )
• ( + ) $\div$ ( - ) = ( - )
• ( - ) $\div$ ( + ) = ( - )
• 어떤 수를 0으로 나누는 경우는 생각하지 않는다.

역수를 이용한 나눗셈

역수

두 수의 곱이 1이 될 때, 한 수를 다른 수의 역수라 한다.

$ \frac{3}{2}$ x $\frac{2}{3}$ = 1 이므로 $ \frac{3}{2}$의 역수는 $\frac{2}{3}$이고, $\frac{2}{3}$의 역수는 $ \frac{3}{2}$이다.
0에 어떤 수를 곱하여도 1이 될 수 없으므로 0의 역수는 없다.

 

 

역수를 이용한 나눗셈
나누는 수를 그 수의 역수로 바꾸어 곱셈으로 고쳐서 계산한다.

역수를 이용한 나눗셈

 

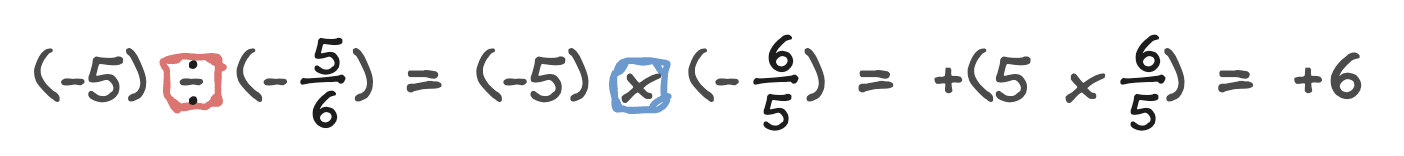
역수 구하기

 

1. 정수는 분모를 1로 고쳐서 역수를 구한다.
   -2( = $-\frac{2}{1}$ ) → -$\frac{1}{2}$
2. 소수는 분수로 고쳐서 역수를 구한다.
   1.5( = $\frac{3}{2}$ ) → $\frac{2}{3}$
3. 대분수는 가분수로 고쳐서 역수를 구한다.
   $1\frac{1}{2}$( = $\frac{3}{2}$ ) → $\frac{2}{3}$